Why your Homegrown IRR Math is Probably Way Off and Causing you Problems you Don't Even Realize

Even some experienced investors don't realize that IRR (internal rate of return) and annual return aren't the same thing. So when they create homegrown calculations with IRR, they nearly always come to very inaccurate conclusions. This simple-to-make mistake can lead an investor to take on more risk than they realize, or unnecessarily pass on a deal that was actually attractive to them.

(Usual disclaimer: I'm just an investor expressing my personal opinion and not a registered financial advisor, attorney or accountant. Consult your own financial professionals before making any financial decisions. Code of Ethics: We do not accept any money from any sponsor or platform for anything, including postings, reviews, referring investors, affiliate leads or advertising. Nor do we negotiate special terms for ourselves in the club above what we negotiate for the benefit of members.).

Background: What is IRR?

As investors, we all look at investments differently because of our unique financial situations and risk tolerances. But every investor cares about one thing: how much money the deal will put in their pocket at the end.

So, almost every sponsor helps investors look at this by providing the IRR ("internal rate of return") of the deal. For example: "After five years, this deal projects a 10% IRR". IRR has become an industry standard and you'll see it in virtually every alternative investing deal (including real estate, private equity, venture capital, litigation finance, life supplements, royalties etc.). And the idea is that you can use IRR to compare deals. A 5% IRR deal projects a lower return than a 10% IRR deal. Simple, right?

But this ubiquitous and simple-sounding metric is actually very misunderstood. And that can cause some dangerous confusion.

"You say tomato, I say tomat-oh"

The problem is that "internal rate of return" sounds a lot like "annual return". So most investors think they're the same. If they hear an investment has a 10% IRR, they believe that's the same as a 10% annual return.

Occasionally, they can be right (which we'll talk about in a minute). But in the world of alternative investing, they're almost always not. And when that happens it can be dangerous.

Here's the important difference between the two.

"The Incredible Lightness of the Annual Return"

Most of us learned in grade school what an annual return is. If you invest $100 in a CD and get back $5 more at the end of the year, you've made a 5% annual return. It's so simple that a child can both understand and calculate it.

Now, here's the definition of IRR from investorpedia:

"The internal rate of return is a discount rate that makes the net present value (NPV) of all cash flows from a particular project equal to zero. IRR calculations rely on the same formula as NPV does."

After reading that, you might be saying: "Huh? What the heck does that even mean?"

And that's the point I'm trying to make. IRR is super complicated and very different than annual return (and CAGR, APR, % return and all of the other numerous things people usually confuse it with). That's because it incorporates a much more abstract concept called the time value of money (NPV).

This is a fiendishly difficult thing to calculate. It so hard, it can't even be calculated with what we typically think of as a "normal" formula and has to be done through something called recursion (which is a process where a formula is repeated over and over again and after many many trials and errors eventually narrows in on the final answer). This is so complex that, before spreadsheets were invented, IRR was very rarely even used.

Let's take a look at this nasty formula for how to calculate IRR (and the commentary from Investopedia):

No one is going to want to take on that beast of a formula by hand. So, obviously, IRR is a completely different animal than annual return and the two have nothing to do with each other.

So how do I use IRR properly?

IRR is only intended to be used to compare with other IRR's. In other words, a 10% IRR is a higher return than a 5% IRR and vice versa. That's it. It is not supposed to be used to compare with annual returns.

Or to put it another way: a 10% IRR does not necessarily mean a higher return than a 5% annual return. Maybe it is and maybe it isn't. But you can't compare the two because they are entirely different measurements.

It's like trying to ask whether 10 inches is more or less than 5 hours. It's a nonsensical question. because the two metrics have nothing to do with each other.

But many investors don't realize the above. And that can get them into trouble when looking at deals.

When calculating from "gross" can get gross

Virtually every responsible sponsor will report the IRR as "net". This means that it is the IRR the investor gets after all of the sponsor fees, profit splits etc. However, occasionally a sponsor will only report the IRR as "gross". This means before all of those fees and profit splits are deducted. And when that happens, it's a pet peeve of mine, because the investor needs the net IRR to do their due diligence. I personally will always go back to the sponsor and try to ask for the net IRR before going further. But I've seen that many investors believe that they can create a homegrown calculation where they calculate the NET IRR themselves by mixing IRR's with annual percentages. And when they do, they can go dangerously off the tracks.

Another situation where I've seen this happen is when a sponsor reports both gross and net and the investor believes that as part of due diligence they will "reconcile"/double-check the difference. Again, they do this by mixing IRR with annual percentages and they get into the exact same trouble.

"Show me the numbers!"

I'll give you an example of how to calculate IRR the wrong way vs the right way. (And the huge difference between the two).

Let's say an investor's looking at a deal that projects a 10% gross IRR, and they want to figure out the net IRR. They don't understand that IRR and annual return are completely different things and should not be mixed together in a calculation.

Here's what they will do:

(For this example, I assumed a typical private equity structure with 2% management fee and a waterfall with an 8% preferred return, return of capital and 80% investor/20% sponsor split. I also assumed a pretty typical case of several capital calls occurring in the first couple of years, an initial "dry period" of no distributions for 2 years, and then distributions which increase from there...but are not entirely the same amount each time).

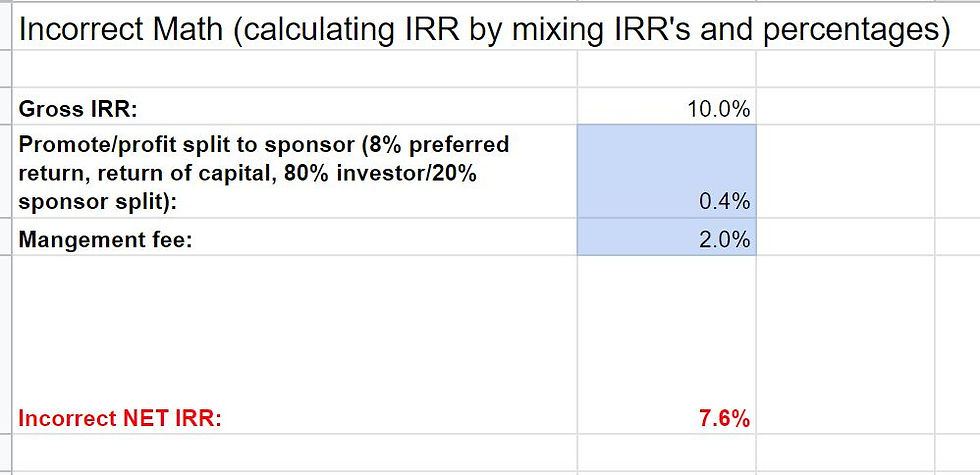
This was really easy to calculate because all they did was subtract percentages from IRR's. The "answer" they got is 7.6% net IRR. And unfortunately it's way off from the accurate answer.

Here's how to calculate it the right way.

(It's a lot of work. You must load every single capital call and distribution into a spreadsheet; subtract out the management fee, which is pretty quick and easy, and then the sponsor split, which is a little bit more work; and finally, run the IRR formula on it -- and thank the Excel makers that you don't have to do the recursive formula by hand. Also, it's important to remember to use the XIRR function, aka the variable date IRR feature, of the spreadsheet, versus just the plain IRR function. The plain IRR function will give inaccurate answers because the capital contribution and distribution dates aren't at 100% regular intervals.)

After taking the time to do the above, the actual answer is 4.9% net IRR. So that's a big difference from the homegrown answer of 7.6% net IRR.

In this particular case, the investor's mistake might've caused them to take on a lot more risk than they realized. But this isn't always the case, and in some situations they might under-calculate the actual return. In that case, they might unnecessarily pass on a deal that actually met their requirements. And as you can see, doing it right is a lot of work. So whenever I run into an investor who tells me, "I quickly did an IRR calculation and it says..." it brings up an immediate yellow flag for me. In general, there is no such thing as a quick IRR calculation, and they are probably making an inaccurate calculation.

Can IRR and annual return ever be the same?

Rarely, yes, internal rate of return and annual return are pretty much the same thing.

An example is a CD where:

1. All money is put in entirely at the very beginning.

2. The distributions are going to be the exact same amount and made at exactly regular intervals.

In this case, the net IRR and the annual percentage are probably going to be the same or at least pretty close.

But, almost no alternative investment is exactly like that.

1. Many times, the money isn't put in via a lump sum at the beginning. Instead, the money is collected from the investor in smaller chunks (called "capital calls") that might be spread over a time period as long as 1-5 years.

2. Many times, the distributions are very different from a CD's, and aren't going to be exactly the same amount each time. There may be an initial period at the beginning where there are no distributions expected at all (the "dry period"). When they do start, many times they start off lower and then increase (the "ramp up"). And many times, the final distribution is expected to be many times larger than anything made previously.

So, this is why mixing IRRs and annual percentage returns is usually a dangerous thing to do.